LDA

Linear Discriminant Analysis

This algorithm can be used for dimensionality reduction to avoid over fitting and reduce computations cost. It also can be used as a classifier. Given a dataset with d-dimensions, the FLD (short for Fisher Linear Discriminant, Fisher is the inventor of this method) tries to find the best directions that could provide best separation between the classes of data. As illustrated in the figure below, one direction could provide a very good separation between classes if our data is projected along it while another may not be a good one. So, the FLD helps in identifying such direction(s). Even though this is illustrated for 2D space, the idea can be extended for higher dimensionality.

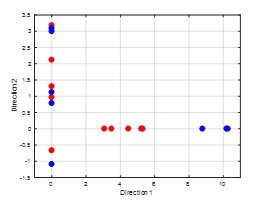
Suppose we have n vectors for our data each is of d-dimensions where d is a high dimension, we first find the mean vectors for each class. We then calculate the eigenvectors and eigenvalues for the scatter matrices, both within class one and between class one. We are interested in such a calculation because we would like to know which direction can give us maximum distance between classes and minimum one within the class and this can be obtained from the eigenvectors that have highest eigenvalues.  Finally we project our original data along these directions.

Examlpe
Let’s assume we got some data that belongs to different classes as follows:
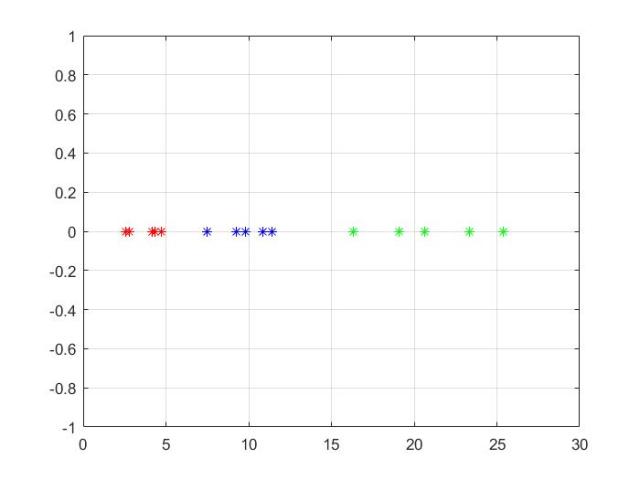
Class X1 = (x,y) = {(2, 3), (3, 6), (4, 4), (4, 2), (2, 4)}, X2 = (x,y) = {(6, 8), (9, 5), (9,
10), (8, 7), (10, 8)} and X3 = (x,y) = {(23, 14), (15, 8), (17, 12), (19, 10), (22, 9)}

MATLAB code:

close all
clear all
clc
X1=[2, 3; 3, 6; 4, 4; 4, 2; 2, 4];
X2 = [6, 8; 9, 5; 9, 10; 8, 7; 10, 8];
X3 = [ 23, 14; 15, 8; 17, 12; 19, 10; 22, 9];
figure
plot(X1(:,1),X1(:,2),'r*')
hold on
plot(X2(:,1),X2(:,2),'b*')
plot(X3(:,1),X3(:,2),'g*')
grid on
Mu1 = mean(X1)';
Mu2 = mean(X2)';
Mu3 = mean(X3)';
S1 = cov(X1);
S2 = cov(X2);
S3=cov(X3);
% within class scatter matrix
Sw = S1 + S2+S3;
% between-class scatter matrix
Mux=[Mu1 Mu2 Mu3];
Mo=mean(Mux,2);
Sb = (Mu1-Mo)*(Mu1-Mo)'+(Mu2-Mo)*(Mu2-Mo)'+(Mu3-Mo)*(Mu3-Mo)';
% LDA projection
SwSb = inv(Sw)*Sb;
% projection vector
[V,D] = eig(SwSb);
% sort according to eigenvalues
eigen_val = diag(D);
[eigen_val_sorted, index] = sort(eigen_val,'descend');
W1 = V(:,index);
% project data samplesalong he projection axes
new_X1 = X1*W1;
new_X2 = X2*W1;
new_X3 = X3*W1;
% get back the original data
old_X1 = new_X1*W1';
old_X2 = new_X2*W1';
old_X3 = new_X3*W1';
figure
plot(new_X1(:,1),new_X1(:,2),'r*')
hold on
plot(new_X2(:,1),new_X2(:,2),'b*')
plot(new_X3(:,1),new_X3(:,2),'g*')
grid on
% reduce dimension
figure
plot(new_X1(:,1),0,'r*')
hold on
plot(new_X2(:,1),0,'b*')
plot(new_X3(:,1),0,'g*')
grid on
figure
plot(old_X1(:,1),old_X1(:,2),'r*')
hold on
plot(old_X2(:,1),old_X2(:,2),'b*')
plot(old_X3(:,1),old_X3(:,2),'g*')
grid on